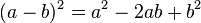lunes, 30 de mayo de 2016

APUNTES GEOMETRÍA

ÍNDICE
1. El triángulo
2. Lugares geométricos 
3. Movimientos en el plano 
4. Resumen de áreas y volúmenes de figuras conocidas 
5. La esfera y el globo terráqueo 
6. Bibliografía

 1.-El triángulo 
1.1 Propiedades y tipos de triángulos
 Los triángulos son figuras geometrícas que se forman por la union de tres segmentos de rectas llamados lados y tres puntos no alineados llamados vértices.

1.2 Rectas y puntos notables en el triángulo (http://gaussianos.com/los-centros-del-trianguloincentro-baricentro-circuncentro-y-ortocentro/)

  • Incentro
El incentro es el centro de la circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma (el radio de dicha circunferencia).
  • Baricentro
El baricentro de un triángulo es el punto de intersección de las medianas de dicho triángulo (siendo una mediana el segmento que une un vértice con el punto medio del lado opuesto). Por ello, para representar gráficamente el baricentro debemos dibujar las tres medianas y localizar el punto en el que se cortan.

                                            

  • Circuncentro
El circuncentro de un triángulo es el centro de la circunferencia circunscrita al triángulo, por lo que la distancia a cada uno de sus vértices es la misma (el radio de dicha circunferencia). En concreto, es el punto de intersección de las mediatrices del triángulo (siendo una mediatriz la recta perpendicular a un lado que pasa por el punto medio del mismo) 
                                             
  • Ortocentro
El ortocentro de un triángulo es el punto de intersección de las tres alturas del triángulo (siendo una altura el segmento que parte de un vértice y es perpendicular al lado opuesto a dicho vértice).
          Ortocentro

1.3 El teorema de Pitágoras

El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos
Pythagorean right angle.svg
Si un triángulo rectángulo tiene catetos de longitudes  a \, y  b \,, y la medida de la hipotenusa es  c \,, se formula:

c^2 = a^2 + b^2 \,
De la ecuación se deducen fácilmente tres corolarios de verificación algebraica y aplicación práctica:
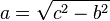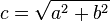a = \sqrt {c^2 - b^2} b= \sqrt{c^2-a^2} c = \sqrt {a^2 + b^2}


1.3.1Demostración de Pitágoras

Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir:
a^2 + b^2 = c^2\,
Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera:
                           (a-b)^2 = a^2 - 2ab + b^2 \,
                                 (b-a)^2 = (a-b)^2 \, .
Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor:

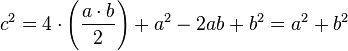
c^2 = 4 \cdot \left( \frac{a \cdot b}{2} \right) + a^2 - 2ab + b^2= a^2 + b^2
Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir:
a^2 + b^2 = c^2\,
Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera:
(a-b)^2 = a^2 - 2ab + b^2 \,
Ya que (b-a)^2 = (a-b)^2 \, .
Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor:
c^2 = 4 \cdot \left( \frac{a \cdot b}{2} \right) + a^2 - 2ab + b^2= a^2 + b^2
Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir:
a^2 + b^2 = c^2\,
Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera:
(a-b)^2 = a^2 - 2ab + b^2 \,
Ya que (b-a)^2 = (a-b)^2 \, .
Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor:
c^2 = 4 \cdot \left( \frac{a \cdot b}{2} \right) + a^2 - 2ab + b^2= a^2 + b^2
Con lo cual queda demostrado el teorema.

1.3.2 El teorema en 3D

Pitágoras 3D
Consideremos el triángulo ABC y los cuadrados construidos sobre sus lados. Digamos que los construidos sobre los catetos tienen áreas a1 y a2 y el construido sobre la hipotenusa tiene área a3. Entonces, según el teorema de Pitágoras tenemos:
                                                 
                                                          a1 + a2 = a3
Si consideramos los prismas que tienen como base los cuadrados y el triángulo, sus volúmenes se calculan multiplicando el área de la base por la altura (h). Entonces, los volúmenes de los prismas son:
V1 = a1 · h
V2 = a2 · h
V3 = a3 · h
En términos algebraicos, podemos establecer que, cuando ‘h‘ es distinto de cero, se cumple:

a1+ a2= a3⇒ h · a1+ h · a2= h · a3⇒ V1 + V2 = V3
Esta es una conclusión algebraica, pero quiere decir que, el volúmen del prisma que contiene la hipotenusa, es igual a la suma de los volúmenes de los prismas que contienen los catetos del triángulo ABC.

1.4 El teorema de Tales (vídeo: Les Luthiers - Teorema De Thales https://www.youtube.com/watch?v=UbalEyegXbQ), triángulos semejantes. ¿Cómo calcular la altura de un árbol a partir de su sombra?

Es una similitud al problema de cómo calcular la altura de un árbol a partir de su sombra sin embargo en este problema calculamos la altura de el edificio y del árbol.

2. Lugares geométricos 

2.1 ¿Qué es un lugar geométrico?

Un lugar geométrico es un conjunto de puntos que satisfacen determinadas condiciones o propiedades geométricas.

2.2 La mediatriz y la bisectriz 

Mediatriz: Es la recta que pasa por el punto medio de un segmento y es perpendicular a él.
                  Los puntos de la mediatriz están a la misma distancia de los extremos  del                             segmento
                                  
                                           

Bisectriz: Es la recta que divide un ángulo en dos ángulos iguales .
                 Los puntos de la bisectriz están a la misma distancia de los lados del ángulo.
                                               

2.3 Las cónicas

.2.3.1 ¿Qué es una cónica?

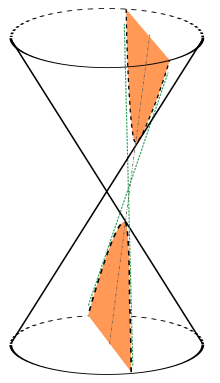
Las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola,hipérbola y circunferencia

2.3.2 La circunferencia

Si el plano que corta a la superficie cónica es perpendicular al eje, la sección es una CIRCUNFERENCIA 

                                                                    Generación de una circunferencia

2.3.3 La elipse: 

Si inclinamos el plano de modo que sea oblicuo con el eje (o directriz) y corte a todas las generatrices, la sección es una elipse.

                                                               Generación de una elipse

 Obtención en un cono








 Método del jardinero 

Se basa en la definición más corriente de la elipse. Los clavos o las chinchetas se colocan en el lugar de los focos, y la cuerda debe medir lo mismo que el eje mayor.

 Mesa de billar elíptica

Se trata de una mesa de billar en la que las bandas rectas han sido sustituidas por una única banda contínua de forma elíptica. Es un dispositivo presente en algunos museos de ciencia que ya había fabricado, entre otras ideas ingeniosas, Lewis Carrol . Su característica principal es que cualquier bola lanzada desde un foco, o que pase por él, acaba pasando por el otro foco después de rebotar en la banda.


Resultado de imagen de mesa de billar eliptica

2.3.4 La hipérbola:

 Obtención en un cono

 La lámpara hiperbólica 

  • Se define como origen al filamento del foco o bombilla de la lámpara.
  • Los ejes x e y forman el plano horizontal con el eje x paralelo a la pared y el eje yperpendicular a la pared.
  •  El eje z es el eje vértical.
                                       

2.3.5 La parábola:

 Obtención en un cono

 El horno solar 

 El espejo parabólico

3. Movimientos en el plano

3.1 Las translaciones. ¿Qué es un vector?


Segmento de recta, contado a partir de un punto del espacio, cuya longitud representa a escala una magnitud, en una dirección determinada y en uno de sus sentidos.

"la longitud de un vector indica, a escala, la magnitud que representa"

3.5 Frisos, mosaicos y cenefas


Frisos:




Mosaicos:

Cenefas:
Resultado de imagen de cenefas

3.6 MC. Escher

Maurits Cornelis Escher (1898-1972). más conocido por sus iniciales como M.C. Escher, es uno de los más grandes artistas gráficos del siglo XX. Tal vez la mejor definición que se ha dado de él sea la de «uno de los más reconocibles y admirados por el gran público». Sus más populares obras, figuras imposibles, fondos reticulados con diversos patrones y mundos imaginarios han sido reproducidas hasta la saciedad en portadas de libros, revistas, campañas publicitarias y en todo tipo de formatos. Escher es, en cierto modo, uno de los artistas más referenciados en la «cultura popular» del siglo XX.
Tal vez el carácter matemático de sus obras ha hecho también que sea uno de los artistas más populares en los entornos científicos, especialmente matemáticos e informáticos. Curiosamente, sus conocimientos matemáticos siempre fueron muy limitados. Muchas de las conclusiones gráficas y matemáticas a las que llegó, que le permitirían realizar algunos de sus trabajos, tuvo que descubrirlas por sí mismo.
Los expertos coinciden, y es bastante evidente examinando la mayor parte de sus obras, en que una de sus principales características es la dualidad y la búsqueda del equilibrio, la utilización del blanco y el negro, la simetría, el infinito frente a lo limitado, el que todo objeto representado tenga su contrapartida.
El análisis de sus obras, tal y como definió Bruno Ernst, uno de sus biógrafo, permite clasificarlas básicamente en tres temas y diversas categorías:

  • La estructura del espacio - incluyendo paisajes, compenetración de mundo y cuerpos matemáticos.
  • La estructura de la superficie - Metamorfosis, ciclos y aproximaciones al infinito.
  • La proyección del espacio tridimensional en el plano - Representación pictórica tradicional, perspectiva y figuras imposibles.

Las obras más conocidas de Escher son probablemente las figuras imposibles, seguidas de los ciclos, metamorfosis y, directa o indirectamente, sus diversos trabajos sobre la estructura de la superficie y la partición regular del plano (patrones que rellenan el plano).

4. Resumen de áreas y volúmenes de figuras conocidas


5. La esfera y el globo terráqueo 

5.1 Elementos principales de la esfera.

●Centro: Punto interior que equidista de cualquier punto de la esfera.
●Radio: Distancia del centro a un punto de la esfera.
●Cuerda: Segmento que une dos puntos de la superficie.
●Diámetro: Cuerda que pasa por el centro.
●Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.

5.2 Elementos de la esfera terrestre

EJE DE ROTACIÓN: La Tierra tiene forma esférica y da vueltas sobre sí misma. La línea recta imaginaria que pasa por el centro de la esfera terrestre (representado en la figura 1 por el punto G) y alrededor de la cual gira la Tierra se llama eje de rotación.
POLOS: El eje de rotación corta la superficie de la Tierra en dos puntos P y P´ (fig. 1). Estos puntosson respectivamente el Polo Norte y el Polo Sur.ECUADOR: El plano perpendicular al eje que pasa por el centro de la Tierra se llama ecuador.También se utiliza este término para designar el círculo que este plano determina en la superficie terrestre y que divide a la Tierra en dos mitades iguales (hemisferios).HORIZONTE DE UN PUNTO O: Es el plano tangente a la superficie terrestre en ese punto.LÍNEA MERIDIANA DEL PUNTO O: Es la línea que en el horizonte del punto O marca la dirección norte-sur.
                                                 
Además de estas líneas imaginarias, sobre la Tierra se trazan una red de líneas que sirven para localizar cualquier punto de su superficie. Estas líneas son los paralelos y los meridianos.
PARALELOS: Son círculos paralelos al ecuador. Como puedes ver en la figura 2, los paralelos no
son iguales en longitud.
MERIDIANOS: Son círculos máximos, iguales en longitud entre sí que pasan por ambos polos.
                               













5.3 Los husos horarios, la hora local solar y oficial

Los husos horarios o zonas horarias son cada una de las veinticuatro áreas en las que se divide la Tierra. Esta gira alrededor de su eje una vez cada 24 horas, por lo que se establecen 24 husos horarios.

Todos los husos horarios se definen en relación al Tiempo Universal Coordinado (UTC), por lo que se centran en el meridiano de Greenwich (0º). Al pasar de un huso horario a otro en dirección Este hay que sumar una hora y por el contrario, al pasar de Este a Oeste hay que restar una hora.

La línea internacional de cambio de fecha, marca el cambio de día. Esta es una línea imaginaria se traza sobre el Océano Pacífico, coincidiendo con el meridiano de 180º. Atravesar este meridiano supone el cambio de fecha, exactamente un día.

Generalmente, los husos horarios están centrados en meridianos de una longitud que últiplo de 15°; sin embargo, como consecuencia de las fronteras políticas, las delimitaciones pueden seguir líneas que adoptan formas muy irregulares.

Algunos países agregan una hora en verano (horario de verano), para así aprovechar la luz solar. Los países del hemisferio norte agregan esa hora en marzo o abril y los países pertenecientes al hemisferio sur, lo hacen en octubre o noviembre.

Existen países que poseen su propio huso horario, por lo que no siguen el patrón que marca el Tiempo Universal Coordinado.

5.4 El método de Eratóstenes para calcular el diámetro de la circunferencia terrestre (vídeo Carl Sagan https://www.youtube.com/watch?v=4gpECWx8sns)

 Eratóstenes realizó observó que, en Alejandría, el mismo día y a la misma hora no se producía este mismo hecho. Asumió de manera correcta que el Sol se encontraba a gran distancia y que sus rayos, al alcanzar la tierra, lo hacían en forma (prácticamente) paralela. Esto ratificaba su idea de que la superficie de la Tierra era curva pues, de haber sido plana, no se hubiese producido esta diferencia entre las dos ciudades. El siguiente paso fue medir en Alejandría el ángulo que formaban los rayos del sol con la vertical que por construcción es igual al ángulo cuyo vértice está en el centro de la Tierra (ver gráfico superior). Este ángulo resulto ser de 7º 12' ( = 7'2º) que unido al hecho conocido de que la distancia entre las dos ciudades era de 5.000 estadios, dieron como conclusión que la circunferencia de la Tierra medía 360·5000/7'2; es decir, 250.000 estadios. Aunque no se tienen datos exactos, se sabe que el estadio equivale a unos 160m (actualmente se suele tomar 158m). Por tanto, 250.000 estadios son aproximadamente 250.000*160/1000 = 40.000 Km. Esto equivale a un radio de 6.366 Km. o 6.286 si tomamos los 158m, contra los 6.371 Km. que son los admitidos hoy en día.
        Las únicas herramientas de Eratóstenes fueron palos, ojos, pies y cerebro, y además el gusto por la experimentación. Con estos elementos dedujo la circunferencia de la Tierra con un error bastante pequeño, lo que constituye un logro notable para el año en que tuvo lugar.

      Publicado por en No hay comentarios:
      Suscribirse a: Entradas (Atom)